WinnER
A Winner-Take-All Hashing-Based Unsupervised Model for Entity Resolution Problems. My B. Sc. Thesis.

for Entity Resolution Problems
Open full paper:
Abstract
In this project, we propose an end-to-end unsupervised learning model that can be used for Entity Resolution problems on string data sets. An innovative prototype selection algorithm is utilized in order to create a rich euclidean, and at the same time, dissimilarity space. Part of this work, is a fine presentation of the theoretical benefits of a euclidean and dissimilarity space. Following we present an embedding scheme based on rank-ordered vectors, that circumvents the Curse of Dimensionality problem. The core of our framework is a locality hashing algorithm named Winner-Take-All, which accelerates our models run time while also maintaining great scores in the similarity checking phase. For the similarity checking phase, we adopt Kendall Tau rank correlation coefficient, a metric for comparing rankings. Finally, we use two state-of-the-art frameworks in order to make a consistent evaluation of our methodology among a famous Entity Resolution data set.
Model corpus
This work builds on the paper Entity Resolution in Dissimilarity Spaces by Vassilios Verykios and Dimitris Karapiperis, architects of this model corpus. They created an efficient and really robust model, that makes unsupervised learning into string ER data sets, with great space and time complexity. Our work, focuses mainly on experiment and finally improve certain parts of the initial idea. Within that approach, we used the theoretical proofs from the paper to convert the initial Dissimilarity space into a Euclidean-Dissimilarity space. In addition, we performed some optimizations to the prototype selection algorithm (Algorithm 1), where we discovered and resolved a vulnerability. In comparison to similar ER clustering frameworks, the key distinctive feature of this model, is the use of a hashing schema in combination with the rank-ordered transformation of the initial data. Moreover, in this study, we offer a detailed presentation of the framework described in the initial paper, as well as our modifications and the results we managed to achieve. This framework is an open-source project, as we also developed an end-to-end model, using Python.

Space Construction is the first part of this model. Input string data, must now be converted into a space of objects. There are plenty of algorithms for prototype selection, however, many of them are sensitive to data variability and so they cannot perform equally well in diverse data sets. In order to circumvent this situation, a Dissimilarity Space Of Objects will be build.
We examine and compare prominent string metrics, like Edit and Jaccard distance and from this research, we present a novel distance stemming from the study in paper Metric and Euclidean properties of dissimilarity coefficients. This study demonstrate that a metric can be both euclidean and dissimilarity at the same time. Nevertheless, from a more theoretical and detailed perspective, a euclidean distance that yields a dissimilarity score has a lot of potential. We should emphasize at this point that we will conduct a deep study of the string distance selection because it is at the heart of our model’s prototype selection phase. We call this hybrid string distance Euclidean-Jaccard, and we will present how it works both theoretically and experimentally.
Vantage Embeddings is the second part of our model. At this point we have created a schema that generates a set of prototypes from a given data set. It is now needed to transform the initial strings into numerical arrays. In Pattern Recognition, this method is called vectorization and the vectors are also called embeddings. Embeddings are a number of vectors, one for each string, that describes it, in a unique way. In our case we want to produce a vector (imagine it like a list of numbers) for every string. In this model we will adopt an embedding technique based on the Vantage Objects. The basic idea of the Vantage Objects comes from the paper, Efficient image retrieval through vantage objects, by J. Vleugels and R. C. Veltkamp. They first mentioned and used a method called Vantage Objects in order to create an efficient object indexing. The Prototypes generated in the previous step of the model will be the Vantage Objects in our study.
Winner-Take-All Hashing is the third and possibly the most important part of the model. In terms of time and memory complexity, entity resolution problems are quite demanding. This is due to the fact that numerous comparisons must be perfromed in order to determine which objects are similar and which are not. Consider a problem using a data set of 1,000 strings, which is considered extremely small nowadays. If we want to find which strings are the same as real-world entities, in a brute force way, we would compare each string with all the others. This means we would have to do 1,000,000 comparisons only to complete this task. This method would take a long time to complete and would require a lot of computing resources. As a result, a hashing method is utilized in this work, which can minimize the number of comparisons to 10% in many cases. Following the previous example, this model can produce predictions with 100,000 comparisons and fairly good scores.
This strategy is also called blocking and is a technique for splitting sets of records into smaller subsets using a criteria function (i.e. a hashing method), with only records belonging to the same block being checked for matches. All records with the same blocking key are placed into the same block in standard blocking, where they are compared pairwise. In Entity Resolution problems, blocking is a common strategy. It may be used to solve ER issues in a single set or to link records from different sets. Furthermore, blocking is a strategy used in cutting-edge frameworks with a proven performance boost, as evidenced by the papers The return of JedAI: End-to-End Entity Resolution for Structured and Semi-Structured Data Eliminating the redundancy in blocking-based entity resolution methods.
We make a detailed presentation of the model scores to the CORA data set and present its superiority among other applications in the same data set. Our criteria are the four scores Recall, Precision, F1 and Accuracy as well as the time needed in order to make these predictions.
Starting, by evaluating this model upon the CORA data set. We will not only present the results from this data set, but we will also give a quick evaluation of each component of the model separately. We will examine the prototype selection, display the embeddings, observe WTA acceleration, and finally remark on the results and see how the similarity metrics we suggested worked. Keep in mind that in order for our model to work, it must be fine-tuned. The fine-tuning will be done with the help of Optuna, a cutting-edge framework. We will go over how we used it and why it is so crucial in our work in a few words. Finally, we will examine the performance of various different ER models and compare them to ours. These models will be created using JedAI, another state-of-the-art framework.
Hyper-parameters
WinnER has the bellow five hyper-parameters: |Parameter|Description| |—|—| | Max number of clusters | Number of maximum clusters that will be created in Prototype Selection phase. Upper bound and the real number of clusters that will be formed will be less than this parameter.| | Max dissimilarity distance | The maximum distance between two strings that can join a cluster. The conditions are met if the distances between the strings being compared are smaller than this threshold. | | Window size or K | This is the WTA hashing hyper-parameter. After the permutation, K is the number of elements that will be selected. | | Number of hashings | Number of WTA-hashing executions.| | Similarity threshold | Threshold of similarity checking phase. If the similarity metric between two rank-ordered vectors is greater than this threshold then these elements are considered same. |
Demonstration
We provide useful python notebooks for demonstration of our framwork in the bellow datasets:
|Dataset|CORA|CDDB|CENSUS|
|—|:-:|:-:|:-:|
| Link to Python Notebook|


Results on CORA dataset
Optuna tuning
Optuna is hyper-parameter tuning framework, famous in the area of Data Science and particularly in Deep Learning. We utilized this tool for our hyper-parameter tuning. Starting with the bellow plot in which we see all the tries made by Optuna and the highest F1 scores achieved.

We also created plots that visualize the classification statistics in order to avoid low recall and high precision or the opposite. In the diagram bellow it is obvious that in the trials with the highest F1-score we managed very good scores both among the same and different entities.
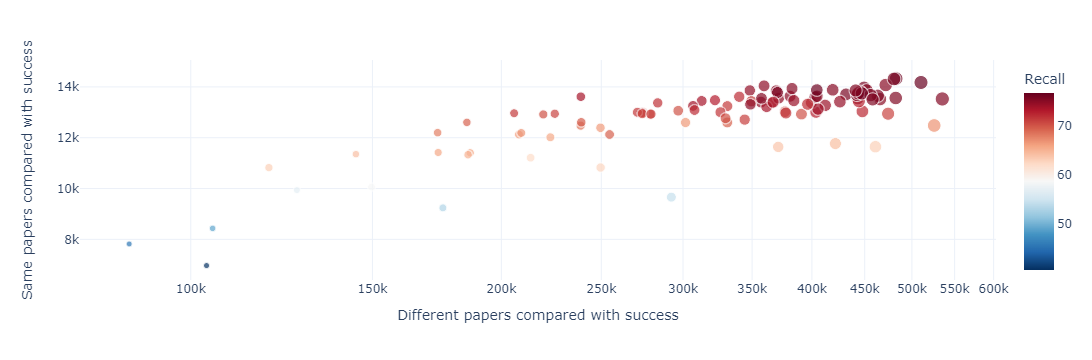
Lastly, we present our best scores:
| Trial id | Recall | F1 | Precision | Accuracy |
|---|---|---|---|---|
| 97 | 87.02 | 79.05 | 72.43 | 99.06 |
| 87 | 86.91 | 79.16 | 72.68 | 99.06 |
| 95 | 86.91 | 79.11 | 72.60 | 99.06 |
| 88 | 86.30 | 79.12 | 73.05 | 99.07 |
| 96 | 86.28 | 78.88 | 72.64 | 99.05 |
| 37 | 84.71 | 79.05 | 74.11 | 99.08 |
| 65 | 84.56 | 78.92 | 73.98 | 99.07 |
| 84 | 84.41 | 78.77 | 73.83 | 99.07 |
| 83 | 83.95 | 78.78 | 74.21 | 99.07 |
| 41 | 82.65 | 78.77 | 75.24 | 99.09 |
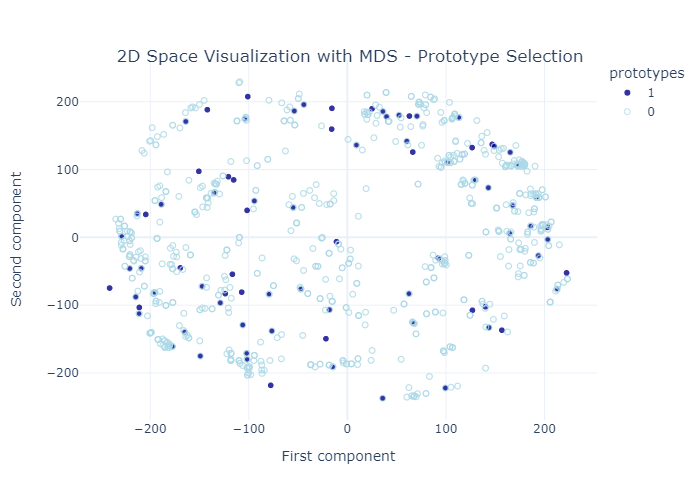
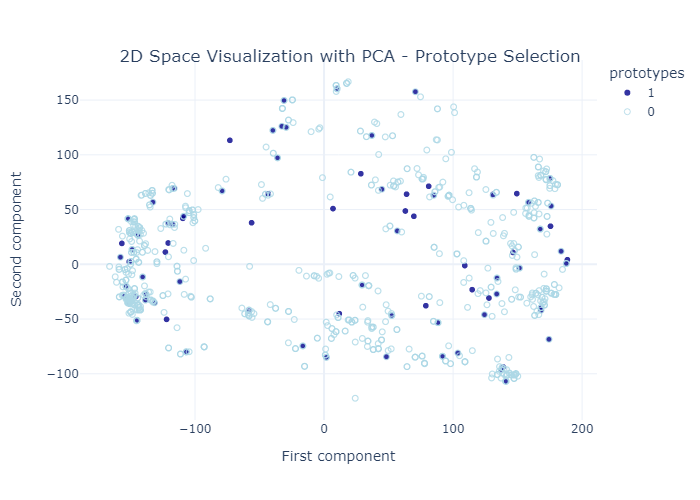
Prototype selection evaluation
As part of this work we also examined the prototype selection algorithm, by visualing it and evaaluating it using the MMD critic. Bellow figures depict the selected prototypes among the overall dataset.
Comparison with JedAI toolkit
In order to evaluate the model we have developed, it is much needed to compare it with other existing models, developed for Entity Resolution. In this study, we utilized a state-of- the-art toolkit named JedAI. JedAI, is a toolkit for Entity Resolution that implements numerous state-of-the-art, domain-independent methods, and provides an intuitive Graph- ical User Interface that can be used for ER experiments and evaluation on data sets.
In this part, we compare our models performance to other well-known ER algorithms. All of these models were created quickly and efficiently with JedAI, which is simple to use and gives consistent results in order to conduct our experiments. Following table summarizes some of the workflows.
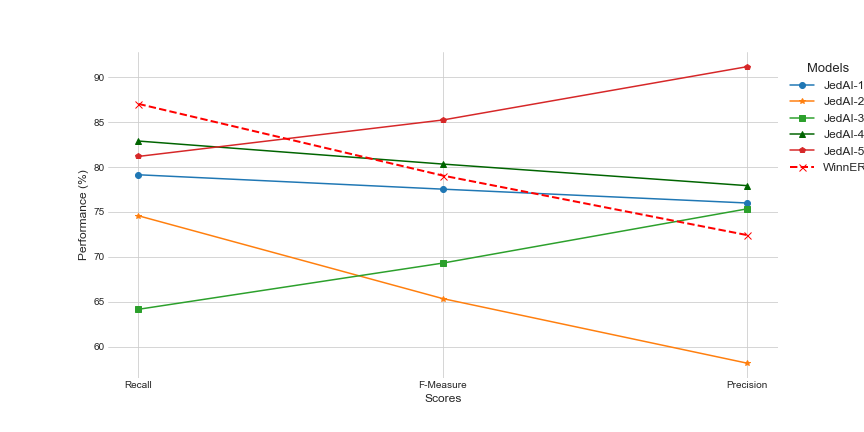
The above figure depicts all the scores shown in the previous table in comparison with our model. WinnER has the greatest Recall score when compared to the other models. However WinnER receives a low Precision score at the same time as it is obvious from the above figure. This comparison demonstrates us the ability of our model to predict with high accuracy the similar pairs, while keeping Precision above 70%.
| # | Block Building | Block Cleaning | Comparison Cleaning | Entity Matching | Entity Clustering | Recall (%) | F-Measure (%) | Precision (%) | Total Time (s) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Standard/Token Blocking, LSH SuperBit Blocking | Block-Filtering, Comparison-based Block Purging | - | Profile Matcher | Merge-Center Clustering | 79.14 | 77.54 | 76.00 | 09:64 |
| 3 | Standard/Token Blocking, LSH MinHash | Size-based Block Purging | - | Profile Matcher | Markov Clustering | 74.58 | 65.37 | 58.19 | 00:47 |
| 3 | Q-Grams Blocking | Comparison-based Block Purging | - | Profile Matcher | Correlation Clustering | 64.18 | 69.32 | 75.35 | 01:09 |
| 4 | Standard/Token Blocking | Block-Filtering | Cardinality Node Pruning (CNP-JS) | Profile Matcher | Connected Components Clustering | 82.89 | 80.33 | 77.93 | 00:11 |
| 5 | Standard/Token Blocking | Block-Filtering | Cardinality Node Pruning (CNP-JS) | Profile Matcher* | Connected Components Clustering | 81.18 | 85.23 | 88.90 | 00:07 |