Winner-Take-All-Hash-Python
Winner Take All Hash in Python
Winner Take All Hash algorithm by J. Yagnik, implemented in Python.This repo contains a brief study on this hashing algorithm.
Original paper: The Power of Comparative Reasoning, Jay Yagnik, Dennis Strelow, David A. Ross, Ruei-sung Lin - 2011
Rank Correlation Spaces
This algorithm benefits the nature of the given embeddings. Embeddings must be rank ordered (partialy or fully). What do we mean when say rank ordered embedding or vector. Lets take an example. Assume $Y$ is our initial vector.
\[Y = [4, -1.5, 2.1, 5.5, 0]\]Then the ranked ordered vector of $Y$ will be:
\[Y_{rankedOrdered} = [3, 0, 2, 4, 1]\]And what’s a rank correlation?
Rank correlation is any of several statistics that measure an ordinal association — the relationship between rankings of different ordinal variables or different rankings of the same variable, where a “ranking” is the assignment of the ordering labels 1st, 2nd, 3rd, etc. to different observations of a particular variable. Rank correlation coefficient measures the degree of similarity between two rankings, and can be used to assess the significance of the relation between them. Rank correlation measures are known for their stability to perturbations in numeric values while giving a good indication of inherent similarity / agreement between items / vectors being considered.
Partial order rankings
There’s no need to have embeddings or vectors of full rankings. For example $Y$ is a full ranking as it has all indexes from 0 to 4. Partial rankings miss a number of that indexes.
Goal
WTA algorithms goal is a feature space transformation that results in a space that is not sensitive to the absolute values of the feature dimensions but rather on the implicit ordering defined by those values. In effect the similarity between two points is defined by the degree to which their feature dimension rankings agree.
Algorithms main functionality
Takes as input a set of vectors (embeddings), and for each vector:
- Permutes with a random pemutation
- Takes the first K components from the permuted vector
- Finds and outputs the index of the maximum value of that components
- Repeats for every vector in the set
The maximum index is the hash code.
A simple pairwise-order measure
The algorithms main point is to make a feature space transformation that benefits the most from the ordering of the vectors. In effect the similarity between two points is defined by the degree to which their feature dimension rankings agree. As an example, Yagnik’s proposal is a measure like the above:
Equation 1:
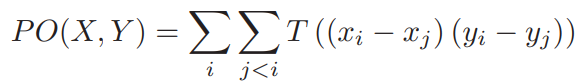
where:
- $x_i$ and $y_i$ are the i-th feature dimensions in
- $X,Y$: ranked ordered vectors
- $T$ is simply a threshold function
Equation 1 simply measures the number of pairs of feature dimensions in X and Y that agree in ordering.
Comparison with MinHash
WTA is a generalization of the well-known MinHash and should enjoy the theoretical benefits of LSH schemes. MinHash is a special case of WTA when applies to binary feautures.